Andrea Lesavourey, Tuong-Huy Nguyen, Adeline Roux-Langlois and myself published on 13^th October 2021 our pre-print (ePrint:2021/1384) titled Log-S-unit lattices using Explicit Stickelberger Generators to solve Approx Ideal-SVP, as well as the associated source code (github:ob3rnard/Tw-Sti). The abstract follows:

The Twisted-PHS algorithm to solve Approx-SVP for ideal lattices on any number field, based on the PHS algorithm by Pellet-Mary, Hanrot and Stehlé in 2019, was introduced in 2020 by Bernard and Roux-Langlois. The authors performed experiments for prime conductors cyclotomic fields of degrees at most 70, reporting the exact approximation factors reached in practice. The main obstacle for these experiments is the computation of a log-S-unit lattice, which requires classical subexponential time.

In this work, we extend these experiments to 210 cyclotomic fields of any conductor m and of degree up to 210. Building upon new results from Bernard and Kučera on the Stickelberger ideal, we construct a maximal set of independent S-units lifted from the maximal real subfield using explicit Stickelberger generators obtained via Jacobi sums. Hence, we obtain full-rank log-S-unit sublattices fulfilling the role of approximating the full Twisted-PHS lattice. Notably, our obtained approximation factors match those from the Twisted-PHS team in small dimensions, when it is feasible to compute the original log-S-unit lattice.

As a side result, we use the knowledge of these explicit Stickelberger elements to remove almost all quantum steps in the CDW algorithm, by Cramer, Ducas and Wesolowski in 2021, under the mild restriction that the plus part of the class number verifies h_m⁺ ≤ O( m^1/2 ).

In the context of post-quantum cryptography and of the NIST competition, a natural target for cryptanalysis is the Ideal-SVP (Ideal Shortest Vector Problem) which asks for a shortest (non-zero) vector in lattices coming from fractional ideals of number fields. Since the buzzing note of Campbell, Groves and Shepherd [CGS14] and the discovery of new number theoretic polynomial-time quantum algorithms [BS16], this problem has gathered more and more attention on how the strong algebraic structure of these lattices could be used to tackle Ideal-SVP, or at least beat traditional lattice reduction algorithms.

For our purpose, it is important to keep in mind two important lines of works:

• The CDW algorithm, by Cramer, Ducas and Wesolowski [CDW17,CDW21], provably solves, in quantum polynomial time in cyclotomic fields of degree n, Ideal-SVP for approximation factors exp Õ( n^1/2 ), under carefully justified heuristics. This algorithm uses the Stickelberger ideal of a cyclotomic field, a special ideal providing free short relations in the relative part of the ideal class group, which can be used to find a close principal multiple for any challenge ideal, i.e., a principal multiple whose algebraic norm is relatively small when divided by the challenge ideal norm. Then, the [CDPR16] routine — a folklore reduction using algebraic units, specifically designed and proven for cyclotomic fields — can be applied to a generator of this multiple, in the hope that it is sufficiently short.
• These two steps can actually be combined in a unique CVP instance: the idea is to find in this way a principal multiple which is not only of small algebraic norm, but is also generated by a small element. This was the core idea of the PHS algorithm by Pellet-Mary, Hanrot and Stehlé [PHS19]. Provided one is ready to pay for an exponential precomputation, they proved that Ideal-SVP can be solved in cyclotomic fields for approximation factors exp Õ( n^α ) in quantum time exp Õ( n^1-2α ), for α ∊ [0, 1/2]. A key ingredient of this proof is to use a CVP with pre-processing algorithm due to Laarhoven [Laa16].

In fact, the particular lattice used in the PHS algorithm corresponds to a special lattice called the log-S-unit lattice, i.e., a lattice obtained by applying a suitable logarithmic embedding on S-units, where S can be identified to a factor base of prime ideals. As it turns out, choosing carefully the used logarithmic embedding is particularly important in practice.

Indeed, using explicitly this S-unit formalism, A. Roux-Langlois and myself [BR20, Th. 4.1] showed that including the standard number theoretic weights to the coordinates of the logarithmic embedding, yielded an algorithm, which we called the Twisted-PHS algorithm, that provably reached the same asymptotic trade-off between runtime and approximation factor than the PHS algorithm, also using Laarhoven's algorithm. Rationale also indicated that the Twisted-PHS algorithm was better encoding, as a CVP instance, the optimization problem of searching for a principal multiple of small algebraic norm while still minimizing the size of its generator. This is for the theoretical part.
More compellingly, on the practical side, we provided a fully functional end-to-end implementation of the Twisted-PHS algorithm, where Laarhoven's CVP oracle is replaced by Babai's Nearest Plane algorithm [Bab86]. This allowed, for the first time, to run completely an S-unit attack on a significant range of concrete examples. Our experiments for prime conductor cyclotomic fields and NTRU Prime fields of small dimensions, namely up to 70, suggested that:

• under the proper number-theoretic normalization, the log-S-unit lattices at hand have a very particular geometric behaviour and seem very easy to reduce [BR20, §5.1–2];
• the obtained exact approximation factors increase very slowly with the dimension [BR20, Fig. 1.1(5.3) and 5.4], in a way that could reveal subexponential or even better.

To our knowledge, these were the first experimental evidence of the geometric peculiarity of properly normalized log-S-unit lattices and of the practical potential of S-unit attacks. Unfortunately, due to the classical complexity of computing S-units, the attained dimensions are not sufficient to conjecture the practical asymptotic behaviour of the Twisted-PHS algorithm.

Towards experimental data in higher dimensions

In our work, we push experiments to (almost) all cyclotomic fields of any conductor and of degree up to 210. This effectively breaks the small dimension barrier and reaches ranges of parameters where asymptotic phenomena — like the exponential growth of the class number, start to express.

How is this achieved?

The starting point was to remark that the proof of Stickelberger's theorem for cyclotomic fields is completely explicit: for each Stickelberger relation in the ideal class group, the proof exhibits an explicit number field element that generates the corresponding principal ideal, expressed via some combinations of Gauss or Jacobi sums that are efficiently computable.

Now, let S be a factor base of full Galois orbits of split prime ideals of the m-th cyclotomic field K_m. We prove (Th. 3.13) that a full rank family of independent S-units can be obtained simply from a set of fundamental S⁺-units of the maximal real subfield K_m⁺ by adjoining, for each Galois orbit of S, the explicit principal ideal generators corresponding to a basis of the Stickelberger ideal. In that way, we obtain a full-rank sublattice of the log-S-unit lattice in K_m at the — classically — much smaller cost of computing S⁺-units in the maximal real subfield, which has dimension only half! This is mostly what allows us to reach dimension 210.

We also give (again in Th. 3.13) an explicitly computable formula for the index of this S-unit multiplicative subgroup modulo torsion. Roughly, simplifying to the case where S generates the whole class group, it writes as:

h_m⁺ · (h_m^-)^d-1 · 2^b · (2^n/2-1+a)^d ,

where d is the number of distinct Galois orbits in S, n = φ(m) is the degree of K_m and a and b are two explicit positive integers that only depend on the prime factorisation of m.

Mitigating the sublattice index

Unfortunately, the index given above is huge, so we only obtain a degraded version of the Twisted-PHS algorithm using a sparse log-S-unit sublattice.

For small prime factors though, classical saturation techniques have the power of mitigating this issue: typically, performing 2-saturation will yield a denser log-S-unit sublattice, whose index is precisely the former one divided by all powers of 2 that occur in its prime factorisation. We shall see in the following that this small densification has a significant impact on the finally obtained approximation factors. Note however that large prime integers are hidden in h_m^-, the relative part of the class number, so that applying this strategy to reach the full S-unit group, thus reducing the index to 1, seems a priori hopeless, even in the medium dimensions that we reach. For example, the relative class number of the 197^th cyclotomic field of degree 196 is divisible by 9398302684870866656225611549, a 93–bits prime!

This is still not the end of the practical hurdles we have to tackle. The 2-saturation process involves computing square roots of products of the number field elements at hand, and this quickly becomes intractable as the bit sizes of these elements coefficients grow. In order to climb dimensions as far as possible, this motivates to constrain both the number of elements we use and their size. This is where the following result comes particularly handy: Radan Kučera and myself identified a large family of short Stickelberger relations [BK21, Pr. 3.1], encompassing the family previously identified in [CDW21, §4.2], and from which it is computationnally easy to extract a short basis of the Stickelberger ideal [BK21, Th. 3.6] for any cyclotomic field. As it happens, principal ideal generators associated to these short relations are always expressed by Jacobi sums [BK21, Pr. 5.1], and these are particularly easy to compute. Hence, this short Stickelberger basis reveals extremely useful to contain the coefficients growth and obtain denser log-S-unit sublattices up to degree 210.

Experimental observations

So, for almost all cyclotomic fields of degree up to 210, we built all log-S-unit sublattices corresponding to the full-rank independent family of Th. 3.13 (urs), its 2-saturated counterpart (sat) and, when computationnally feasible, i.e. up to degree 80 at the moment, a fundamental system of the full S-units group. We also varied the number d of full Galois orbits of the factor base from 1 to the optimal value d_max predicted by the Twisted-PHS algorithm. By optimal, we mean here the value such that the density of the full log-S-unit lattice is maximal.

We stress that pushing experiments up to dimension 210 is a significant breakthrough. To our knowledge, no other experiments of S-unit attacks beyond dimension 70 have been publicly reported since [BR20].

Geometry of the log-S-unit lattice

First, the very peculiar geometric characteristics observed in [BR20, §5.1–2] — small orthogonality defect (after LLL), shape of the log norms of the Gram-Schmidt basis, ease of reduction — are consistently viewed across all conductors, degrees, log-S-unit sublattices and number of orbits.

For example, the following figure plots a typical shape of the Gram-Schmidt log norms of the log-S-unit sublattice, before and after a reduction by BKZ with blocksize 40. This one was obtained for prime conductor m = 211, for the 2–saturated family on d = 5 Galois orbits of split prime ideals. The BKZ–40 reduced basis of this 1154–dimensional lattice was obtained in about 7 (!) minutes on a single CPU core.

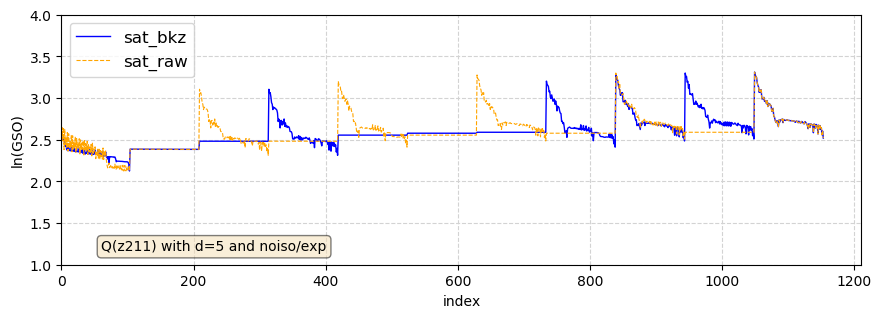
These recurrent observations in very different regimes suggest that this phenomenon has a possibly deep explanation, an observation that has been recently developed by Bernstein and Lange [BL21].

Approximation factors

Second, we ran the (practical version of the) Twisted-PHS algorithm using our log-S-unit sublattices on simulated random targets to see how the final approximation factor evolves with the dimension in our degraded regime. Here is the graph that we obtain under the Gaussian Heuristic:

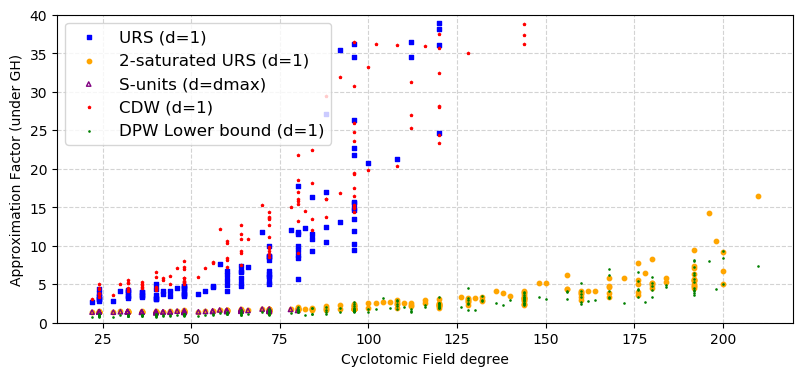
Remark: Note that, for each family of S-units, we chose to plot only the results obtained for the factor base that gives the best result. As we observed a very strong correlation between the density of our lattices and the obtained approximation factors — the denser the better, this systematically translated into using d = 1 orbit for the family of Th.3.13 and its 2–saturated counterpart, whereas we had to plot the curve for d = d_max orbits when using the full S-unit groups, as predicted by the Twisted-PHS algorithm.

For comparison purposes, we plotted in small red points the outcome of the CDW algorithm. As intuitively expected, this is very similar to the curve obtained for the family of Th.3.13. Moreover, the green dots correspond to the volumetric lower bound derived in [DPW19, §6.1–2 and Eq.(5)] using the exact value for the first split prime norm. For some of the fields (e.g. in degree 200), this lower bound is defeated by the (degraded version of the) Twisted-PHS algorithm; note that this does not invalidate the lower bound itself, which is stated for the two-phase CDW algorithm, but indicates the power of combining both steps in only one lattice as in the (Twisted-)PHS algorithm.

We stress that this graph does neither show a catastrophic impact of S-unit attacks, nor does it clear the threat. Indeed, the obtained curve only depicts the performance of the Twisted-PHS in a very degraded mode beyond dimension 80, however valuable is this upper bound on what is reachable in practice.
Nevertheless, those data already suggest a strong correlation between the density of the lattice and the approximation factor obtained by the Twisted-PHS algorithm: the denser, the better. For instance, for m = 211, the blue point is at ordinate 13170 and the corresponding log-S-unit sublattice has reduced volume 14.3, whereas the yellow point at ordinate only 16.4 for the 2-saturated family corresponds to a sublattice of reduced volume 11.4. To give a more complete picture, let us mention that the density of the full log-S-unit lattice is maximal for d_max = 7 orbits, for which the reduced volume is only 9.64. Hence, the Twisted-PHS algorithm might reveal more powerful.

Anyhow, gathering these extensive data is of utmost importance to better understand the performances of this class of attacks, and should be seen as a first step towards getting a sound estimation of the asymptotic behaviour of the Twisted-PHS algorithm, and more generally of S-unit attacks with any kind of parameters. Obtaining such an asymptotic simulator is yet another challenge of its own, which is left for future work.

A side theoretical result.

Incidentally, knowing principal ideal generators corresponding to Stickelberger relations and real S⁺-units trivially removes the intermediate quantum step solving the PIP (Principal Ideal Problem) in the CDW algorithm. More importantly, Th. 3.13 mentioned above also allows to remove all quantum steps performed in the Random Walk of the CDW algorithm, that sends any challenge ideal to the relative part of the class group by means of random multiples. Hence, only two quantum steps remain: a precomputational one to obtain real S⁺-units, and another one to obtain, for each target, some multiplicative decomposition in the class group (Class Group Discrete Logarithm Problem).

Under the mild restriction that h_m⁺ ≤ O( m^1/2 ), which should hold true for most cyclotomic fields, this variant reaches the same provable bounds as the CDW algorithm. However, lifting the need to work in the relative class group allows to choose a factor base of ideals with smaller norms and avoids dealing with a small multiple of the challenge, two useful consequences that should improve in practice the obtained approximation factor.

Bibliography

[Bab86] L. Babai: On Lovász' lattice reduction and the nearest lattice point problem. Combinatorica, 6(1), pp. 1–13, 1986.
[BK21] O. Bernard and R. Kučera: A short basis of the Stickelberger ideal of a cyclotomic field. ArXiv pre-print arXiv:2109.13329 [math.NT], 2021.
[BLNR21] O. Bernard, A. Lesavourey, T.-H. Nguyen and A. Roux-Langlois: Log-S-unit lattices using Explicit Stickelberger Generators to solve Approx Ideal-SVP. Cryptology ePrint Archive ePrint:2021/1384.
[BR20] O. Bernard and A. Roux-Langlois: Twisted-PHS: Using the Product Formula to Solve Approx-SVP in Ideal Lattices. In ASIACRYPT, vol. 12492 of LNCS, pp. 349–380, Springer, 2020. Available at ePrint:2020/1081.
[BL21] D.J. Bernstein and T. Lange: Non-randomness of S-unit lattices. Cryptology ePrint Archive ePrint:2021/1428, 2021.
[BS16] J.-F. Biasse and F. Song: Efficient quantum algorithms for computing class groups and solving the principal ideal problem in arbitrary degree number fields. In SODA, pp. 893–902, SIAM, 2016.
[CDPR16] R. Cramer, L. Ducas, C. Peikert and O. Regev: Recovering short generators of principal ideals in cyclotomic rings. In EUROCRYPT, vol. 9666 of LNCE, pp. 559–585, Springer, 2016. Available at ePrint:2015/313.
[CDW17] R. Cramer, L. Ducas and B. Wesolowski: Short Stickelberger Class Relations and Applications to Ideal-SVP. In EUROCRYPT, vol. 10210 of LNCS, pp. 324–348, Springer, 2017. Available at ePrint:2016/885.
[CDW21] R. Cramer, L. Ducas and B. Wesolowski: Mildly Short Vectors in Cyclotomic Ideal Lattices in Quantum Polynomial Time. J. ACM, 68(2), 2021. Available at Archive ouverte HAL:03102234.
[CGS14] P. Campbell, M. Groves and D. Shepherd: Soliloquy: A cautionary tale, 2014. Available at ETSI Crypto Workshop October 2014.
[DPW19] L. Ducas, M. Plançon and B. Wesolowski: On the Shortness of Vectors to be found by the Ideal-SVP Quantum Algorithm. In CRYPTO, vol. 11692 of LNCS, pp. 322–351, Springer, 2019. Available at ePrint:2019/234.
[Laa16] T. Laarhoven: Sieving for closest lattice vectors (with preprocessing). In SAC, vol. 10532 of LNCS, pp. 523–542, Springer, 2016. Available at arXiv:1607.04789 [cs.CR].
[PHS19] A. Pellet-Mary, G. Hanrot and D. Stehlé: Approx-SVP in Ideal Lattices with Pre-processing. In EUROCRYPT, vol. 11477 of LNCS, pp. 685–716, Springer, 2019. Available at ePrint:2019/215.