The fifth edition of the FPLLL days was held last week (Oct 28th - Nov 1st) at Royal Holloway, University of London. It aimed at bringing together researchers working on lattice algorithms and their implementations; while originally initiated to maintain the FPLLL library itself, it now welcomes any software development projects related to lattices. It was attended by 23 participants who quickly started to collaborate on projects.

Software Releases 
The work performed during this meeting has lead to the release of new versions of FPLLL and FPyLLL:

FPLLL 5.3.0:
https://groups.google.com/forum/#!topic/fplll-devel/3QebEjcDPs0

FPYLLL 0.5.0dev:
https://groups.google.com/forum/#!topic/fplll-devel/Bp1eUnsdF6E

Dual mode for G6K (Léo Ducas & Michael Walter)

It is suspected that for certain problems (e.g. BDD, LWE), reducing the dual lattice rather than the primal lattice can be advantageous. Indeed, while the typical analysis treat the profile of log-Gram-Schmidt norm as a straight line (Geometric Series Assumption), it is in fact known to have a small concavity [YD17, BDW18]. By switching to the dual we can turn it into convexity. Yet the potential gain remains to be studied both in theory and in practice.

The goal of this project was to enable this research direction within the current fastest lattice reduction library, namely the Generalized Sieve Kernel [ADPS18]. This was already realized a few years ago for the FPLLL enumeration algorithm, by working on the dual in an implicit manner. It turned out that this approach would be rather painful to implement in G6K. Instead we still avoid the computation of the full dual basis by only computing the dual on the current considered block, directly on the Gram-Schmidt decomposition. By doing so, we committed what is considered a cardinal sin in numerical linear algebra, namely explicitly inverting a triangular system. This will certainly backfire in largish dimension, trigger numerical stability issues down the road … but we were still happy to plot this.

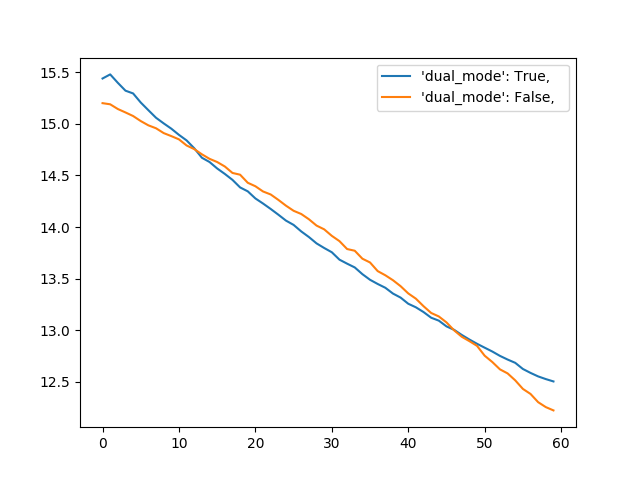
• [YD18] Second Order Statistical Behavior of LLL and BKZ, Yang Yu, Léo Ducas, (SAC 2017)
• [BDW18] Measuring, simulating and exploiting the head concavity phenomenon in BKZ, Shi Bai and Damien Stehlé and Weiqiang Wen (Asiacrypt 2018)
• [ADPS18] The General Sieve Kernel and New Records in Lattice Reduction, Martin R. Albrecht and Léo Ducas and Gottfried Herold and Elena Kirshanova and Eamonn W. Postlethwaite and Marc Stevens (Eurocrypt 2019)

Gram-BKZ (Koen de Boer & Wessel van Woerden)

In the current version of fplll, SVP and BKZ and LLL-reduction can be applied on lattices represented by a Gram matrix alone. Indeed, some lattices are better represented as quadratic forms, and writing them with a lattice basis would naively involve irrational numbers. This generalization may find application to reduce lattices arising as ideals in CM number fields, or in the study of dense lattice packing and perfect forms~[Woe18,Sch09].

Also, these modules (SVP,BKZ,LLL) now accept a more general Gram-Schmidt-object [MatGSOInterface], making way for implementing a more numerically stable GramSchmidt orthogonalization using Givens rotations.

[Woe18] Perfect Quadratic forms: an Upper Bound and Challenges in Enumeration, Wessel van Woerden, Master Thesis: https://www.universiteitleiden.nl/binaries/content/assets/science/mi/scripties/master/2017-2018/msc-scriptie-wpj-van-woerden.pdf
[Sch09] Computational geometry of positive definite quadratic forms: polyhedral reduction theories, algorithms, and applications, Achille Schürmann, American Mathematical Society,2009.
The following code gives an example how to apply BKZ on a Gram matrix. [Thanks to @malb for the Python-wiring]

Running yields something like

Implement an iterative slicer out of G6K (Wessel van Woerden, Emmanuel Doulgerakis & Eamonn Postlethwaite)

The iterative slicer is a simple CVPP algorithm where the preprocessing consists out of a large list of short lattice vectors. The best way to obtain such a large list is to use lattice sieving which makes the algorithm a nice fit with G6K. Given a target vector t the iterative slicer tries to repeatedly translate the target to a smaller representative t' in the coset t+L by a lattice vector in the list; t-t' then gives a lattice vector at distance ||t'|| to t. To find the closest vector this process has to be repeated by randomising the target t leading to the so-called randomized iterative slicer [DLW].

We implemented a basic version of the randomized iterative slicer that uses the current sieve database as the preprocessed list. There is ongoing progress in further optimising this, e.g. by reducing polynomial overhead and using nearest neighbour search data structures. We are trying to ensure consistency w.r.t. the other CVP solvers in FP(y)LL

• [DLW] Doulgerakis, E., Laarhoven, T., & de Weger, B. (2019). Finding closest lattice vectors using approximate Voronoi cells. PQCRYPTO. Springer (2019).

Tutorial (Maxime Plancon & Marios Mavropoulos Papoudas)

• C++ tutorial : Autonomous scripts showing how to perform basic operations, such as basis generation methods, LLL reduction and BKZ reduction. Commentary on the use of the flags of each method is provided. In the future, tutorials will include HKZ reduction, slide reduction, SVP and CVP.

• Python tutorial : Reworked the existing python tutorial : reorganisation into sections, adding new examples of functions, displaying latex (the latex expressions are not directly displayed on github, do not know why)

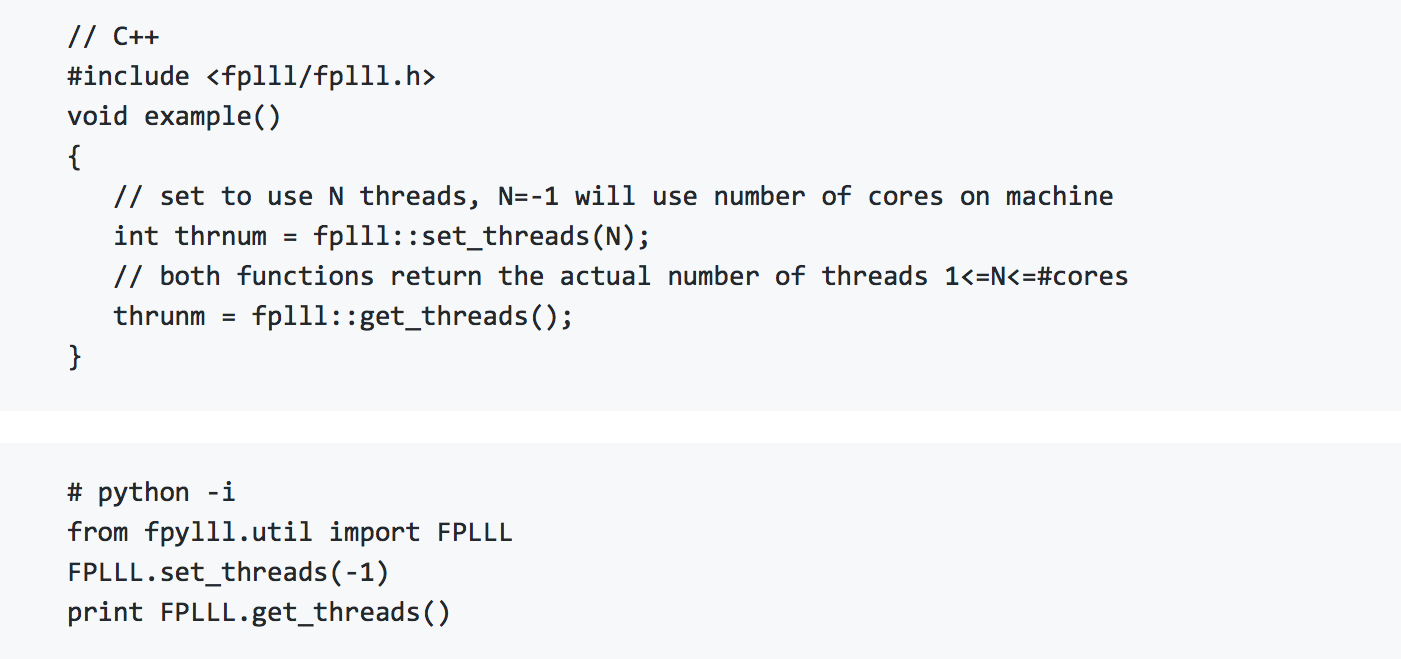
Threadpool & Multithreaded Enumeration (Marc Stevens)

There seem to be repeated efforts to improve single-core FPLLL enumeration with parallel enumeration implementations. FPLLL had only single-core enumeration, but supports external enumeration libraries to allow parallel enumeration implementations, in particular the parallel enumeration library https://github.com/cr-marcstevens/fplll-extenum. We embedded fplll-extenum as an optional feature as fplll/enum-parallel and, if enabled, sets it as the default using the external enumeration API. As fplll/enum-parallel is fully templated and inlined, compilation times will increase significantly. Hence, configure allows setting an upper limit on the compiled enumeration dimensions:

We also moved its C++11 threadpool implementation to FPLLL's core, making it available for all FPLLL subsystems. By default it will use all available cores on a machine.

Additionally, work was started on a simpler parallel enumeration inside FPLLL making effective use of all available API's: threadpool, single core enumeration with and without subtree, and evaluators. The code does not seem to be working fully correctly yet.

Constrained Enumeration (Martin Albrecht)

FP(Y)LLL now supports imposing arbitrary constraints on solutions found using enumeration. For example, the code below insists that the first coordinate of the solution is two.

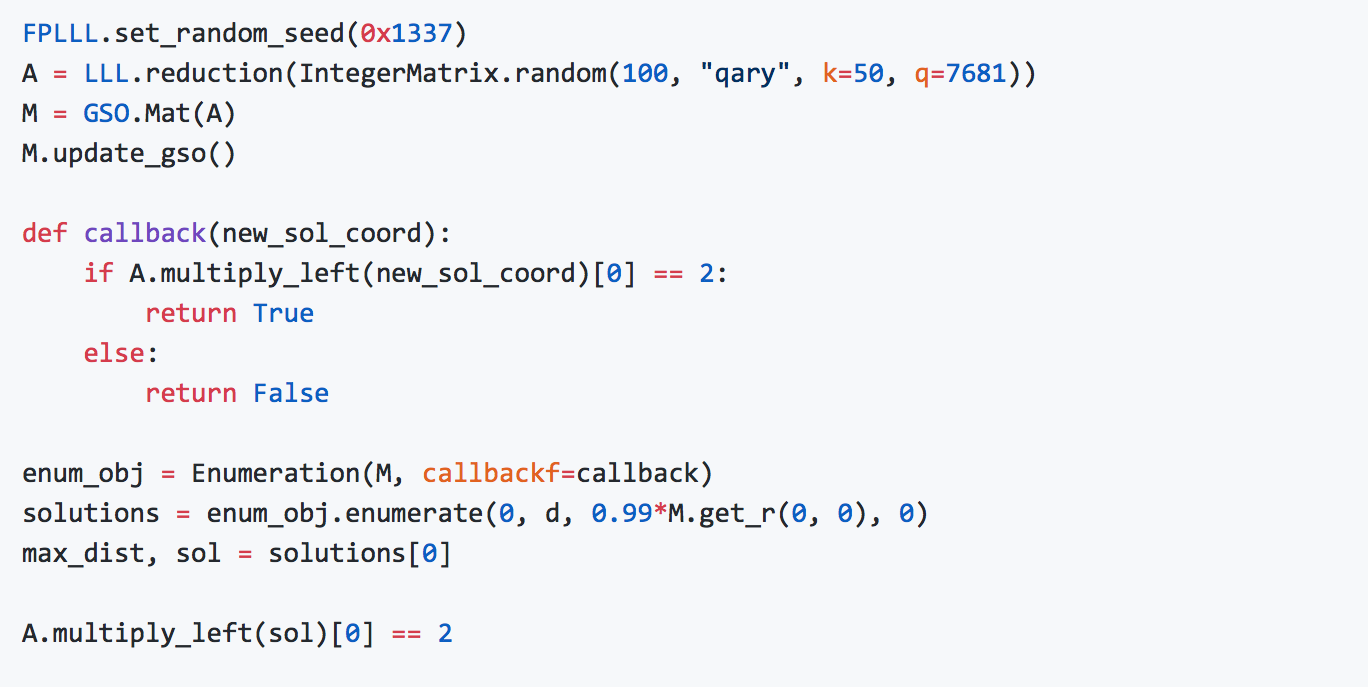
Such constraints can be useful to impose e.g. sparsity or ℓ_∞ norm constraints. It may also be used to implement Minkowski reduction.

Complex-LLL (David Joseph, Christian Porter & Fernando Virdia)

Starting from previous literature GLM06, we worked towards having a Sagemath implementation of LLL over the Gaussian and the Eisenstein integers. We produced an implementation from scratch, and one by porting pre-existing Matlab scripts. Results so far are only partial, since implementations disagree on some specific examples, but the aim is to have them converge into a single correct code base, to use as starting point for larger scale experiments looking at the behaviour of Complex-LLL with regards to output quality bases for equivalent lattices.

L2 in Julia (Chris Peel)

Implemented an L2 of LLL in native Julia which will be added to the Julia package LLLplus. Investigated a Julia wrapper around fplll that would be the Julia equivalent of fpylll; it looks like CxxWrap is the right tool to build such a wrapper.

Distributed SVP solving (Joe Rowell)

Building on previous work such as (https://link.springer.com/chapter/10.1007/978-3-642-15291-7_21), the goal was to build a strong, scalable, open-source implementation of SVP solving. Most of this work was based on theoretical explorations workload distribution amongst nodes - some ideas include the bucketing algorithm from (https://eprint.iacr.org/2015/1128.pdf), work stealing and RDMA. This work remains incomplete, but developments are expected in the near future.

General maintenance work (Martin Albrecht, Marc Stevens)

In addition to developing new features, FPLLL days also serve general maintenance tasks. Overall, 12 support tickets were resolved for FPLLL and 15 pull requests merged (this includes the feature PRs mentioned above). For FPYLLL, four PRs were merged. Configuration for code testing service TravisCI was optimized to decrease waiting times.

Art (Koen de Boer)